Использование метода интервальных оценок для решения задачи
восстановления
статистической информации распределения
занятых по уровню образования и отраслям
экономики внутри субъектов
Российской Федерации
Е. А. Питухин, В. В. Поляков,
Т. С. Терновская
Петрозаводский государственный университет, г. Петрозаводск,
pitukhin@karelia.ru; poljakov.v@karelia.ru; ternov@onego.ru
Для
решения задачи прогнозирования потребностей региональных экономик в
специалистах с профессиональным образованием важным является знание достоверной
информации о распределении занятого населения по уровню образования и отраслям
экономики, которое характерно для исследуемого региона [1, 2].
К
сожалению, статистические данные подобного рода по каждому из 89 СФ отсутствуют
в авторитетных справочниках Госкомстата. Существует такое распределение только
лишь в целом по РФ. Данные можно получить из таблицы
Строки таблицы содержат информацию о 7 уровнях образования:
·
высшее
профессиональное;
·
неполное высшее;
·
среднее
профессиональное;
·
начальное
профессиональное;
·
среднее (полное)
общее;
·
основное общее;
·
начальное общее
или нет образования.
В столбцах таблицы
– 13 укрупненных отраслей экономики:
·
промышленность;
·
сельское и лесное
хозяйство;
·
транспорт и
связь;
·
строительство;
·
оптовая и
розничная торговля, общепит;
·
ЖКХ,
непроизводственные виды бытового обслуживания;
·
здравоохранение,
физкультура, социальное обеспечение;
·
образование;
·
культура и
искусство;
·
наука и научное
обслуживание;
·
финансы, кредит,
страхование, пенсионное обеспечение;
·
управление;
·
другие отрасли.
На
пересечении столбцов и строк – процентная доля выбранного уровня образования
внутри выбранной отрасли экономики.
Попытка напрямую применить процентные соотношения по
уровням образования внутри отраслей экономик из общероссийских данных для
расчета абсолютных региональных показателей приводит к грубым несоответствиям
[1].
Это
иллюстрируется сравнением итоговых сумм по строкам, когда суммируется
численность занятых по уровням образования внутри одной отрасли и сравнивается
со статистическими данными о распределении численности занятого населения по
отраслям экономики и социальной сферы. Значения берутся из таблицы 3.4 «Распределение
среднегодовой численности занятых по отраслям экономики»
справочника «Регионы России, 2001» (стр. 76-79).
Таким
же образом сравниваются и процентные соотношения распределения по уровням
образования, когда суммируется численность занятых по
столбцам внутри одного уровня образования и делится на общее количество занятых
в СФ. Эти значения сравниваются с данными, например, из таблицы 3.5
«Распределение численности занятых в экономике регионов Российской Федерации по
уровню образования в 2000 г.» из справочника «Труд и занятость в России, 2001»
(стр. 79-80).
При
сравнении видно существенное несоответствие полученных в результате расчета
значений и «реперных» итоговых данных из Госкомстата. Очевидно, что расчетные данные
должны совпадать со статистическими.
Данное
несоответствие и отсутствие доступных исходных статистических данных по каждому
СФ приводит к постановке задачи достоверного восстановления исходных данных о
распределении занятого населения по уровню образования и отраслям экономики.
Эта
задача сводится к задаче оптимизации при наличии ограничений.
Опишем
таблицу распределения занятого населения по уровню образования и отраслям
экономики для некоторого СФ матрицей 
.
Общероссийскую
матрицу процентных соотношений распределения занятого населения по уровню
образования и отраслям экономики определим матрицей 
с учетом ограничения
на веса коэффициентов:
. (1)
«Реперный»
вектор процентных соотношений по уровням образования примем за 
. Вектор 
распределения среднегодовой
численности занятых по отраслям экономики определим как 
.
Российские
данные используем как некоторые начальные данные для оптимизации в виде матрицы
:
.
Очевидно,
что такая матрица вызовет сильное
отклонение при сравнении результатов ее обработки с итоговым «реперным» вектором
процентных соотношений 
:
,
где
– допустимое
отклонение.
Возникает
задача: найти такую матрицу 
, чтобы отклонения итоговых векторов отличались от
"реперных" и минимальным образом.
Эту
задачу оптимизации можно свести к задаче квадратичного программирования.
Запишем целевой функционал 
как сумму квадратов
разностей отклонений по образованию:
.
Запишем
целевой функционал 
как сумму квадратов
разностей отклонений по экономике:
.
Общий
целевой функционал 
запишем как 
.
Критерий
оптимизации – минимум целевой функции при наличии областных
ограничений:
, (2)
где
– матрица нижних
ограничений;
– матрица верхних
ограничений.
Здесь
– коэффициент
девиации, который задает допустимую область изменения оптимизационных
параметров – коэффициентов матрицы .
Тогда
постановку задачи оптимизации можно было бы записать как:
. (3)
Данная
задача эффективно решается численными методами, например, методом
покоординатного спуска с наличием областных ограничений.
При
этом возникает проблема точности и адекватности определения элементов матрицы .
Кроме
неточного задания функциональных ограничений и , которые имеют тенденцию меняться от года к году, элементы
матрицы также обязательно
будут варьироваться, флуктуировать с течением времени. И если мы делаем прогноз
до 2015 г., то должны учесть возможную флуктуацию элементов
матрицы начиная с 2004 г.
Задача
(3) минимизации квадратичного функционала дает нам максимально точное, «правильное»
решение в детерминированной области. Но, как говорилось выше, ответ (матрица ) получается также детерминированным. При этом возможная
флуктуация ее параметров может привести к нарушению ограничений, как областных
(2) (если решение располагается близко к границе), так и функциональных (1).
Параметры
матрицы было бы ошибочно
считать при прогнозировании строго равными выбранным оптимальным значениям –
они будут флуктуировать из-за влияния факторов, не учтенных при моделировании и
возникших после получения решения. При этом в задачах выпуклого
программирования отклонение любого управляемого параметра от оптимального
значения с вероятностью не менее 0,5 приводит к недопустимой ситуации,
поскольку оптимальное решение всегда находится на границе области допустимых
значений.
Справиться
с отмеченной проблемой возможно путем перехода к моделям, «поглощающим»
неточности, как моделирования, так и реализации решений. К таким моделям
относятся предлагаемые авторами задачи оптимизации с интервальными переменными,
предполагающие возможность произвольного колебания значений управляемых параметров
в определенных интервалах [3]. Решение такой задачи оптимизации представляет
собой многомерный параллелепипед, полностью «погруженный» в область допустимых
решений, любая точка которого является допустимым решением, а координаты центра
определяют значение целевой функции.
Идея
метода заключается в том, что если задачу оптимизации можно свести к линейной
задаче с линейными ограничениями, то решение задачи оптимизации можно получить
не «точкой», а «отрезком», некоторым интервалом.
Очевидно,
что задача определения коэффициентов матрицы может быть также
сведена к линейной, а не квадратичной задаче (3): необходимо решить 7+13
линейных алгебраических уравнений с 
неизвестными.
Поскольку
общее количество занятых в экономике СФ известно из справочных данных, то
величину 
можно заменить на константу без большого ущерба для точности:
.
Получаем
7 уравнений:
, (4)
и
еще 13 уравнений:
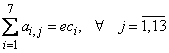. (5)
При
этом сохраняются все ограничения (1).
Система
уравнений (4, 5) решается стандартными методами линейного программирования, при
этом выполняются ограничения (1, 2). К тому же метод интервальных оценок дает
возможность задать коэффициент вариаций 
, который будет определять процентное отклонение от
номинальной точки каждого проектного параметра:
.
Таким
образом, мы получим гиперкуб допустимых (не оптимальных!) решений, любая
реализация которых, тем не менее, не выведет решение за пределы функциональных
ограничений (1).
Ниже
описывается подход, позволяющий получать решения в виде интервальных оценок.
Задача
оптимизации с интервальными переменными включает два непересекающихся
подмножества переменных: подмножество 
обычных (точечных)
переменных 
и подмножество 
интервальных
переменных 
, представляющих в решении непрерывные интервалы значений
(ограничения задачи должны выполняться для любого значения переменных , принадлежащего этим интервалам). Величины 
являются срединными
значениями интервалов. В общем виде модель задачи с интервальными значениями
переменных включает целевую функцию:
(6)
и
два множества (
и 
) ограничений – типа "равенство":
, 
, (7)
включающие
только переменные 
для 
, и типа "неравенство":
, 
, (8)
которые
должны выполняться для всех значений (), определяемых ограничениями вида (7) и любого набора
значений переменных 
(
), если каждое значение попадает в интервал
, ,
где
– ширина интервалов,
задаваемая как относительная величина.
Несомненным
достоинством предлагаемого подхода является то, что в случае линейности
соотношений вида (8) возникающая задача оптимизации не требует специальных методов
решения, поскольку путем модификации легко приводится к задаче линейного программирования.
Для этого каждое из ограничений (8) преобразуется следующим образом:
, .
Здесь
в каждом из ограничений подмножество интервальных переменных разбивается на два – 
, соответствующее неотрицательным коэффициентам 
и 
для отрицательных
коэффициентов . Теперь умножение коэффициентов при интервальных переменных,
относящихся к множествам и , на величины 
и 
соответственно даст
соотношение:
, , (9)
позволяющее
при точечном характере переменных 
множества построить интервальное
решение на основе решения задачи линейного программирования.
Решая
задачу (4, 5) с помощью подхода (9), получим решение в виде матрицы
интервальных элементов =
, где в нашем случае 
, а мощность множеств интервальных переменных и равна числу элементов
матрицы . При этом
, 
, 
.
Применение
такого метода интервальных оценок в процессе восстановления исходной
статистической информации о распределении занятого населения по уровню
образования и отраслям экономики дает возможность более уверенно осуществлять
прогнозирование в периоде среднесрочного планирования. Это делает математическую
модель потребностей рынка труда в специалистах с профессиональным образованием
более адекватной реальности, а получаемые с помощью нее оценки более достоверными.
Список литературы
1.
Гуртов В. А. Моделирование
потребностей экономики региона в выпускниках системы высшего профессионального
образования / В. А. Гуртов, А. Г. Мезенцев, Е. А. Питухин // Регионология. 2003.
№1-2. С. 262-267.
2.
Гуртов В. А.
Математическая модель прогнозирования спроса и предложения на рынке труда в
российских регионах / В. А. Гуртов, Е. А. Питухин // Обозрение прикладной и
промышленной математики. Т. 11. Вып. 3. М., 2004. С. 539.
3.
Поляков В. В. О
возможности использования задач оптимизации с интервальными решениями в
оперативно-диспетчерском управлении / В. В. Поляков, Е. А. Корольков, Р. В. Воронов
// Новые информационные технологии в ЦБП и энергетике: Материалы VI Междунар. научно-технич. конф., г. Петрозаводск,